Rapport de Stage Post-Doctoral
Martial MANCIP
Projet OPALE
ARC Couplage
27 juin 2002
Table des matières
- Table des matières
- 1. Introduction
- 2. Couplage de schémas numériques
- 2.1 Introduction
- 2.2 Définition du couplage
- 2.2.1 Schémas Volumes Finis
- 2.2.2 Projection des solutions approchées
- 2.2.3 Fonction et algorithme de couplage
- 2.3 Équations d'Euler
- 2.4 Cas tests
- 3. Implémentation sur la grille
- 3.1 Notion de parallélisation par boites recouvrantes
- 3.2 Parallélisation d'un code Volumes Finis
- 3.3 Parallélisation d'un code particulaire
- 3.4 Présentation de CAST
- 3.5 Construction des codes
- 4. Conclusion
-
Bibliographie
1. Introduction
Les recherches dans le domaine de l'analyse numérique en France sont souvent très spécialisées dans un domaine de la physique. On commence depuis quelques années à modéliser des phénomènes de fluides complexes ou multi-phasiques. Mais de nombreux projets visent à modéliser des phénomènes très précis, donc utiliser dans des industries très pointues. Peu de projets englobent des modèles radicalement différents (comme l'hydrodynamique et la mécanique des milieux continus, ou l'électromagnétisme, par exemple), sur des grands ensembles.
Un fait d'actualité est très parlant : Le crash en novembre 2001 (pour perte de dérive arrière) d'un avion sur New-York, dont on ne connaît toujours pas les causes officielles est un évènement très problématique pour les constructeurs et les compagnies (ainsi que pour les voyageurs !).
Depuis plus de vingt années, on construit des avions avec des matériaux composites en testant des éprouvettes pour la résistance et le vieillissement de ces matériaux. Par contre on ne savait et on ne sait toujours pas considérer (calculer) l'avion comme une entité globale (aérodynamisme, structure, thermique, électronique, dans un vol complet). On calcule simplement l'aérodynamisme d'une aile ou son vieillissement. Or il est évident que les matériaux, insérés dans une structure globale, soumis à des vols réguliers, ne subissent pas les mêmes contraintes à long terme que celles imposées à une seule partie.
C'est une avancée majeure dans le domaine de la sécurité des passagers qui doit se jouer : comme pour les véhicules terrestres, les avions de lignes doivent être testés globalement avant leur mise sur le marché. Le problème est la taille des calculs. Les avancées en informatique, et plus particulièrement les grappes de PC et le réseau VTHD (Vraiment Très Haut Débit, réseau à plus de 2 Go/s), permettent d'envisager de tels calculs dans un avenir proche. En effet, non seulement cette grille de grappes de PC, mise en place sur trois sites éloignés de l'INRIA, forme une machine parallèle très concurrentielle (classée environ 300ème en 2001), mais elle permet surtout de faire du calcul réparti sur plusieurs grappes de PC et couplés. La cohérence entre le couplage de code (calcul réparti) et le couplage de modélisation (couplage par décomposition de domaines) est totale. Cela améliore les performances et la taille des calculs.
- CAST est un logiciel créé par Toan Nguyen à l'INRIA Rhône-Alpes, au sein du projet SINUS. Cette plateforme organise des tâches dans un ordre prédéfini sur plusieurs grappes de PC. Une tâche peut être un simple exécutable à lancer, une requête CORBA ou des exécutables parallélisés (type PVM ou MPI) qui s'exécutent sur plusieurs nœuds simultanément.
- La décomposition de domaines peut être alors une décomposition avec des recouvrements des sous-domaines (dans le cas d'interactions entre plusieurs modèles fluides, par exemple) ou sans recouvrement (dans le cas d'interactions fluides-structures).
Il est donc important de construire un code de modélisation numérique complet (fluide, thermique, structure, électromagnétisme) adapté à la grille de grappes. Il s'agit dans un premier temps de construire une application distribuée, basée sur un module de couplage parallélisé (client) et un ou plusieurs solveurs fluides VF (VF : solveur Volumes Finis) et SPH (SPH : solveur particulaire - Smooth Particle Hydrodynamics, voir [Lac97 ] ou [Lan00 ]).
Dans la figure qui suit, on a représenté un calcul global de l'aérodynamisme d'un avion et les interactions entre les différents codes gérés par CAST.
Le couplage est parallélisé grâce à des zones de couplage déterminées par l'utilisateur. Celles-ci fournissent la géométrie et les conditions initiales et définissent des zones de solveur (fixes ou mobile, fixes par rapport à un bord) et les zones de couplage entre les solveurs. On utilisera des objets ``zone'' (CORBA-tisé, c'est-à-dire encapsulés dans un objet CORBA, pour permettre les communications entre objets sur grappes distantes) pour chaque résolution numérique et un objet ``couplage'' (CORBA-tisé lui aussi) qui communiqueront entre eux par l'intermédiaire de CAST. Le couplage pourra être VF-VF et VF-SPH.
Les codes de calcul stockeront les éléments (particules ou mailles, modèle, solveur) qu'ils possèdent et qui sont situés sur la zone. Ils seront retournés au code de couplage, qui calculera le couplage de manière parallèle et renverra ces éléments aux codes.
On a donc besoin de créer trois codes parallélisés :
- le code de couplage (FluideGlobal),
- le code Particulaire et
- le code VF
On pourra donner deux versions du calcul des flux dans ce code pour construire les résolutions d'Euler et de Navier-Stokes.
Comme le démontrent Denis Trustram et Pierre-Eric Bernard, dans
la thèse [Ber97
], la répartition des tâches de calcul et celles de communication
d'un code est importante pour l'optimisation d'un code de calcul parallèle.
Le but de la librairie ATHAPASCAN (B. Plateau, projet APACHE - INRIA) est
de construire et d'analyser cette optimisation (concept de multiprogrammation
par processus légers communicants). Dans ce travail, nous avons utilisé
librairie de communication parallèle MPI. Nous avons tenu compte des
conclusions de cette thèse en construisant notre parallélisation
avec une notion de découpage en boites recouvrantes (voir section
3.1
). La position et la taille de ces boites sont optimisées pour égaler
la charge de calcul des processus parallèles. La future transformation
MPI ![]() ATHAPASCAN oblige à ne pas utiliser directement les fonctions d'échange
MPI. On a donc créé un objet ``parallele'' les appelant. Ainsi,
on pourra facilement modifier la bibliothèque et en utiliser une autre.
ATHAPASCAN oblige à ne pas utiliser directement les fonctions d'échange
MPI. On a donc créé un objet ``parallele'' les appelant. Ainsi,
on pourra facilement modifier la bibliothèque et en utiliser une autre.
Plan du rapport
Dans un premier chapitre, nous présentons l'algorithme de couplage complet, ainsi que les tests connus que l'on pourra faire subir au programme distribué.
Quant au second chapitre, il contient les informations sur la programmation et l'utilisation du code FluideGlobal. On a mis l'accent sur la manière dont le solveur parallèle a été programmé, afin d'optimiser les recouvrements des communications par des calculs.
2. Couplage de schémas numériques
2.1 Introduction
Nous allons présenter une nouvelle méthode de couplage de schémas pour les lois de conservation. Les lois de conservation interviennent dans de nombreux problèmes industriels, notamment pour l'hydrodynamique (avec le modèle d'Euler) et l'électromagnétique (modèle de Maxwell). Le couplage de schémas permet non seulement de faire une décomposition de domaines, mais il permet en plus d'utiliser localement des schémas adaptés aux problèmes physiques.
Les méthodes de couplage par recouvrement de domaine existent depuis de nombreuses années ([Sta77 ], [Kre83 ], [BD83 ] et récemment [PS94 ]). Ces méthodes de couplage de schémas numériques pour la résolution des systèmes hyperboliques non-linéaires possèdent actuellement d'importants défauts de stabilité et de précision (voir la thèse d'Eva Pärt-Enander [ Pär95 ]). Cette constatation que nous avons faite avec Jean-Paul Vila (voir ma thèse [Man01 ]), nous a poussés à construire un algorithme de couplage par recouvrement de domaine très novateur. En effet, on fait se chevaucher les domaines sur une zone déterminée, afin de passer d'une méthode numérique à une autre. C'est ce qu'on appelle le couplage par recouvrement de maillage. Le point important concernant cette méthode est qu'il n'y a pas de condition aux limites du domaine de couplage.
Dans le cas scalaire, par exemple, la solution ![]() d'un modèle hyperbolique non-linéaire vérifie :
d'un modèle hyperbolique non-linéaire vérifie :
où la jacobienne du flux ![]() est diagonalisable et à valeurs propres réelles.
est diagonalisable et à valeurs propres réelles.
De plus, nous avons montré théoriquement que dans ce cas scalaire, cet algorithme est stable et convergeant. L'estimation de l'erreur de couplage est négligeable devant celles des schémas Volumes Finis utilisés. (voir [Man01 ], )
2.2 Définition du couplage
On définit donc deux sous-domaines (notés ![]() et
et ![]() ) du domaine complet
) du domaine complet ![]() qui se recouvrent sur une zone (que l'on appellera zone de couplage) notée
qui se recouvrent sur une zone (que l'on appellera zone de couplage) notée
![]() . Ils sont donc tels que :
. Ils sont donc tels que :
Cette zone de couplage ![]() doit surtout être de mesure non négligeable par rapport au
support de la condition initiale
doit surtout être de mesure non négligeable par rapport au
support de la condition initiale ![]() .
.
Sur ces deux sous-domaines, on utilise des maillages quelconques de type Éléments Finis. On ne peut pas avoir l'un des nœuds d'une maille à l'intérieur de l'une des arêtes d'une autre maille. De plus, la triangulation n'est pas dégénérée (aucun triangle n'est aplati).
2.2.1 Schémas Volumes Finis
La solution approchée du schéma Volumes Finis numéro
'![]() ' (
' (![]() ) est obtenue au temps
) est obtenue au temps ![]() de la manière suivante;
de la manière suivante; ![]() :
:
avec 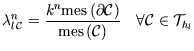 .
.
où ![]() désigne le flux numérique qui calcule la solution élémentaire
1D du système hyperbolique.
désigne le flux numérique qui calcule la solution élémentaire
1D du système hyperbolique.
2.2.2 Projection des solutions approchées
La projection pour des solutions approchées constantes par morceau,
dans la zone de recouvrement (zone de couplage) est
Avec
Le calcul de cette projection est alors réduit, dans le cas de deux maillages fixes, au calcul préliminaire des intersections des mailles de ces maillages, dans la zone de couplage. A chaque pas de temps, on aura une simple multiplication matrice-vecteur à calculer, où la matrice est la matrice des mesures des intersections et le vecteur, le champ à projeter.
2.2.3 Fonction et algorithme de couplage
On définit la fonction de couplage ![]() à l'aide d'une fonction que l'on prolonge par continuité à
tout
à l'aide d'une fonction que l'on prolonge par continuité à
tout ![]() de la façon suivante :
de la façon suivante :
Une représentation possible de cette fonction ![]() est donnée dans la figure 2.1
.
est donnée dans la figure 2.1
.
On définit les deux sous-domaines (vitaux pour la convergence) de
![]() où la fonction de couplage vaut vraiment :
où la fonction de couplage vaut vraiment :
Les résultats théoriques montrent que ces ensembles sont vitaux pour la stabilité de l'algorithme.
On approche alors cette fonction de couplage de la même manière
que pour les Volumes Finis :
|
|
|
|
|
|
Le principe global de l'algorithme est le suivant : on part des solutions
approchées à un instant ![]() donné. On utilise les deux schémas numériques séparément
(opération que l'on note alors respectivement
donné. On utilise les deux schémas numériques séparément
(opération que l'on note alors respectivement ![]() et
et ![]() ), puis on effectue la correction par le couplage (projection
), puis on effectue la correction par le couplage (projection ![]() et
et ![]() ), pour obtenir les solutions à l'instant suivant
), pour obtenir les solutions à l'instant suivant ![]() . On a représenté schématiquement ces étapes
dans la figure 2.2
.
. On a représenté schématiquement ces étapes
dans la figure 2.2
.
Dans cette figure, les étapes ![]() et
et ![]() correspondent aux deux schémas numériques et les étapes
correspondent aux deux schémas numériques et les étapes
![]() et
et ![]() représentent les projections et le couplage.
représentent les projections et le couplage.
Enfin, on définit la solution approchée moyennée :
qui est la solution du problème, valable dans tout le domaine.
2.3 Équations d'Euler
En dimension 3, le système d'Euler (dont la solution ![]() est dans
est dans ![]() ) est tel que :
) est tel que :
|
|
|
avec
|
|
|
![]() désigne la densité,
désigne la densité, ![]() désigne le vecteur vitesse,
désigne le vecteur vitesse, ![]() désigne l'énergie totale et
désigne l'énergie totale et ![]() désigne la pression du fluide. Il s'agit bien d'une loi de conservation
non linéaire où
désigne la pression du fluide. Il s'agit bien d'une loi de conservation
non linéaire où ![]() désigne le flux.
désigne le flux.
On fait alors des hypothèses de comportement sur le fluide, qui
entraînent des lois de comportement :
|
|
|
où l'on définit le paramètre adimensionné
![]() et la vitesse du son :
et la vitesse du son :
|
|
|
|
|
|
|
|
|
|
2.4 Cas tests
Nous disposons d'un certain nombre de cas tests sévères en mécanique des fluides compressibles. Le cas test d'école est le tube à choc de Sod. Il s'agit d'un tube, en théorie infiniment long, qui contient deux gaz aux repos, dont on connaît les conditions initiales.
Lorsqu'on enlève la séparation initiale entre les deux zones, on obtient différentes ondes que l'on sait calculer exactement, du fait de la symétrie centrale du problème :
Le cas test de l'injection d'un gaz dans un autre est un exemple développé dans ma thèse.
Nous pourrons ré-étudier ce cas au travers de ce code multi-fluide, en utilisant les différentes grappes de PC pour les deux schémas Volumes Finis et l'algorithme de couplage. C'est le cas dans les deux figures suivantes :
Dans la figure 2.7 , le jet est déjà formé et l'onde de choc qui le précède va frapper contre la cible.
Enfin dans la figure suivante, on présente le même calcul, avec une modélisation VF-SPH (la méthode particulaire étant utilisée pour la chambre de droite). On a mis la zone de couplage en évidence, dans la figure inférieure droite.
À l'heure où nous rédigeons ce rapport, nous n'avons malheureusement pas encore pu lancer des cas-tests, du fait de la grande complexité de la programmation de ce code de couplage parallélisé, en 3D et en C++. Néanmoins nous présentons la construction de ce code dans le chapitre suivant.
3. Implémentation sur la grille
Le code est organisé comme ceci : il y a une phase d'initialisation
et une phase de calcul. La phase de déclaration comprend les points
suivants :
1
définir la géométrie de base (dimension, forme des objets, bords externes),
2
Déclaration des zones globales
a
modèle parmi une boite
![]() solveur,
solveur,
b
définitions des conditions aux limites,
3
Validation des zones de couplages (qui ne sont pas forcément au bords des zones de calcul). Appel à CAST pour la réservation des solveurs,
4
Calcul des fonctions de couplage et des matrices d'intersections des mailles, si les deux maillages n'évoluent pas dans le temps.
Puis il y une phase de calcul, qui nécessite d'effectuer les points suivants :
5
calcul des schémas au pas de temps,
6
retour des valeurs dans les zones de couplage,
7
phase de couplage : correction sur ces valeurs,
8
renvoie des données corrigées au solveur,
9
mise à jour de l'affichage et sauvegarde globale.
Les codes de calcul stockent les éléments (particules ou mailles, solveurs, maillage) qu'ils possèdent et qui sont situés sur la zone. Les éléments contenus dans une zone de couplage et les valeurs calculées seront retournés au code de couplage. Celui-ci calculera le couplage de manière parallèle et renverra les valeurs modifiées aux codes solveurs.
Les objets couplages sont chargés des tâches suivantes :
- mise à jour des éléments (en fonction des boites que l'objet couplage contient)
- calcule leur fonction de couplage sur les éléments,
- échange objets voisins et calcul du maximum des fonctions de couplage avec leurs voisines (opération maximum sur la fonction de couplage),
- se réduisent après cette communication pour éviter les calculs doubles (règle de la définition sens direct en 2D),
- trouvent les boites qu'ils possèdent et envoient cette information ,
- calculent le couplage
- renvoient les valeurs modifiées à leurs boites respectives
3.0.0.1 Déroulement par code
Dans le cas du couplage de deux solveurs VF, on a deux codes principaux :
![]()
Boites,
![]()
Couplage ou FluideGlobal.
Le code ``Boite'', parallélisé, contient (par exemple au nœud 0), un processus spécial, chargé de la gestion du calcul, que nous nommerons ``Maître'' par la suite.
La phase d'initialisations comporte alors les points suivants :
![]() Maître :
Maître :
ouverture des fichiers de maillage, allocation et lecture,
![]() Maître :
Maître :
lecture des paramètres du cas test, des CI et des zones de couplage,
![]() Maître :
Maître :
envoie les zones de couplage
![]() Maître :
Maître :
calcul des boites et sous-boites,
![]() Maître :
Maître :
envoie les résultats boites et sous-boites,
![]() Boites :
Boites :
attendre l'envoie du maître.
La boucle temporelle contient les actions suivantes :
![]() Boites :
Boites :
calcul des schémas au pas de temps,
![]() Boites :
Boites :
retour des valeurs dans les zones de couplage,
![]() Couplage :
Couplage :
phase de couplage : correction sur ces valeurs,
![]() Couplage :
Couplage :
renvoie des données corrigées aux boites,
![]() Maître :
Maître :
mise à jour de l'affichage et sauvegarde globale.
![]() Maître :
Maître :
re-calcul des boites et sous-boites, si besoin
![]() Maître :
Maître :
envoie les résultats boites et sous-boites,
![]() Boites :
Boites :
calcul le nouveau pas de temps.
3.1 Notion de parallélisation par boites recouvrantes
On créé des objets - boites parallélisées. Ces boites recouvrent le domaine et se recouvrent mutuellement sur leurs bords. Pour plus de compréhension sur cette notion de boite, on utilise un cas test de choc carré, dont on utilise les deux symétries pour obtenir un choc de coin :
au bout d'un certain temps ![]() , la ligne de choc se déplace et s'arrondit :
, la ligne de choc se déplace et s'arrondit :
On doit donc imposer un rangement des boites non régulier, le long des fortes discontinuités initiales. Et on doit aussi savoir le faire avancer. Mais l'onde de choc traverse cette zone en un temps fini. On a donc pas à la modifier à chaque pas de temps.
Au bout d'un temps ![]() , on devra recalculer les positions et les tailles des boites :
, on devra recalculer les positions et les tailles des boites :
Dans le cas d'un maillage lagrangien (particulaire), le rangement est optimisé le long du choc, pour permettre de respecter les propriétés suivantes
-
on veut que toutes les particules dans une boites aient leur
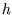 (ie le nombre de voisins) à peu près constant,
(ie le nombre de voisins) à peu près constant, -
et que la taille (pas de grille) soit fonction de
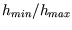 .
.
Ces propriétés garantissent que chaque processus a une charge de calculs à peu près égale. On obtient alors les résultats suivants :
|
|
|
Figure : onde déformée et schéma |
Les intersections des boites forment des objets sous-boites :
- on créé ainsi une hiérarchie des sous-boites (intersection de 2,3,4 ... boites), leur intérieur (les éléments qui n'appartiennent pas à une sous-boite), leur aire et leurs sous-boites (et le nb_sous_boites).
- On classe les sous-boites en fonction de leur aire.
- On descendra l'arbre jusqu'aux feuilles pour calculer les sous-boites les plus basses, et on remontera pour les calculs des éléments intérieurs des sous-boites au-dessus.
Pour la boite ci-dessous, les intersections avec ses boites voisines sont multiples :
Une fois les sous-boites calculées, on peut placer les éléments dans l'arbre, en remontant des feuilles aux branches par exclusions des éléments des listes (i.e. : l'intérieur d'une (sous-)boite est obtenu en recopiant la liste de ses éléments, puis en supprimant de cette nouvelle liste, les éléments appartenant à ses sous-boites). Ce qui veut dire que les feuilles n'ont que des intérieurs (égalité entre la liste des éléments et celle de l'intérieur).
Parallélisation : on a trois types de sous-boites (et leur intérieur)
- les sous-boites de bande
- les sous-boites de coin
- et les intersections de deux coins. Pour simplifier l'ordre de sélection des calculs dans les coins, on autorise des intersections de plus de deux boites, mais on n'effectue les calculs que dans les deux premières boites et en les reportant dans les autres boites.
Les bandes et coin diffèrent à cause de la normale au bord ou au coin pour déterminer qui effectue le calcul du flux de l'arête.
3.2 Parallélisation d'un code Volumes Finis
On a programmé la résolution du système d'Euler dans chaque zone, à l'aide d'un solveur VF standard appelé solveur de Roe.
On utilise la notion de boite pour la parallélisation. Le découpage par recouvrements de boites n'est calculé qu'une seule fois car le maillage fixe au cours du temps. Pour égaliser la charge de calcul, il suffit que les mailles contiennent un nombre de mailles à peu près identique.
On tient compte des remarques de P.-E. Bernard pour l'ordonnancement des tâches de calcul numérique et de communication :
- calcul des flux de bords des boites,
- communication flux de bords,
- recouvertes par les calculs des flux intérieurs,
- intégrations des flux de bords,
- recouvertes par les intégrations des flux intérieurs,
- vérifications des valeurs de bords (pour test temporaire : synchronisation des résultats).
Les calculs de flux aux bords et aux coins sont relativement rapides. On peut alors lancer les communications, tout en calculant le gros du schéma (les interactions à l'intérieur des boites).
3.3 Parallélisation d'un code particulaire
Quant au SPH, pour le rendre parallèle, on décide de le remanier. Nous pourrons alors remplacer le schéma Volumes Finis calculant le jet par cette méthode lagrangienne pour notre test d'injection.
La notion de boites mobiles entraîne l'implémentation d'un algorithme d'optimisation linéaire.
- Le nombre moyen de particules par boite :
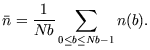
·
La spline ( ![]() ) des nombres de particules :
) des nombres de particules :
·
Les splines des cut-offs min et max :
Le cut-off est le paramètre de recherche des voisins pour le calcul des flux dans ces méthodes particulaires. Cette variable évolue au cours du temps et influence beaucoup la taille des calculs.
Le problème des méthodes sans grille est cette recherche
de voisins dans la zone définie par le cut-off. Elle est coûteuse
en temps de calcul et ne tient ni compte de la physique, ni de la forme du
nuage de points (zones de compression et de détente). Nous nous proposons
de tester un nouvel algorithme SPH, basé sur le tri. Les boites parallélisées
sont quadrillées de telle manière que l'on puisse avoir au plus
une particule par case. En fonction des quadrillages possibles et de la valeur
du cut-off de la particule, on applique un masque prédéfini
(localement admissible) pour trouver ses voisins. Ces masques potentiels sont
calculés une fois au début
![]()
soit du calcul : ils sont
stockés dans le processus maître du code MPI. Une fois la boite
modifiée, le processus maître envoie les formes de cut-off correspondantes
( ![]() beaucoup d'échanges de petites données).
beaucoup d'échanges de petites données).
![]()
soit du pas de temps : ils sont alors calculés localement par la boite, pour être réutilisés par toutes les particules possédant la même taille de cut-off (optimisation des cut-offs calculés, mais beaucoup de mémoire utilisée).
3.4 Présentation de CAST
CAST permet de coupler des codes d'origines diverses en les encapsulant dans des objets CORBA. En utilisant la technologie CORBA, CAST peut interagir avec l'ensemble de ces codes de manière générique et sur des systèmes hétérogènes.
CAST se base sur l'implémentation de CORBA PaCO (qui est une extension de l'ORB Mico développée à l'IRISA pour des objets parallélisés) pour exécuter ces différentes tâches. CORBA est une norme de fait définissant l'implémentation et la communication entre des objets répartis. CORBA permet de s'abstraire complètement des couches réseaux et des systèmes d'exploitation utilisés et d'obtenir une transparence totale dans les appels des requêtes grâce aux invocations dynamiques. CAST utilise les atouts de la technologie CORBA (l'interface de squelettes dynamiques DSI et l'interface d'invocation DII) pour permettre son utilisation sur plusieurs grappes d'ordinateurs simultanément.
3.5 Construction des codes
3.5.1 Choix de programmation
Ces fonctionnalités de CAST nous ont poussés à utiliser le langage C++, comme langage de programmation, de manière à rendre plus naturelle cette encapsulation.
3.5.2 Classes du code
Ensemble des classes qui seront utilisées dans le code (avec l'ordre
de programmation) :
![]()
Gestion : il permet la gestion de la mémoire et des exceptions de tous les objets définis dans chaque code,
![]()
Parallele,
![]()
Maillage,
![]()
MaillageVF hérite de Maillage,
![]()
Boite,
![]()
Sousboites intersections entre les boites voisines,
![]()
Couplage,
![]()
CouplageVFVF hérite du couplage,
![]()
Modele,
![]()
ModeleEuler hérite de la classe Modele,
![]()
Solveur,
![]()
SolveurVF hérite de la classe Solveur (Classe mère des solveurs VF),
![]()
SolveurVFEuler hérite de la classe SolveurVF (contient le solveur de Roe pour le système d'équation d'Euler),
![]()
SolveurVFEulerGodunov hérite de la classe SolveurVFEuler (contient le calcul des flux de type Godunov),
![]()
Zone CORBA englobante,
Lorsque le couplage VF-VF aura été testé, on rajoutera
:
![]()
SolveurSPH hérite de la classe Solveur (Classe mère des solveurs SPH),
![]()
MaillageSPH hérite de Maillage.
![]()
CouplageVFSPH hérite du couplage,
![]()
CouplageSPHSPH hérite du couplage.
La figure suivante présente l'organisation des classes des codes solveurs parallélisés :
On a créé ici une classe de communication : ``Parallele''. Il s'agit des communications de type solveur parallèle (à l'intérieur d'une Zone) et non de celles effectuées entre ces Zones (et remplacées par des objets CORBA).
3.5.2.0.1 Classe Maillage
Description des maillages : variables communes aux VF et SPH
Extrait Maillage : Variables protégées:
$•#bullet;$
dimension du maillage
1
Données maillage -> la lecture est faite par les enfants
· nombre de mailles
· Nombre de nœuds
· Nombre de nœuds pour chaque maille
· Indice des nœuds de chaque maille
· centre des mailles (maillage mobile)
· Coordonnées des nœuds
· Surface des éléments
· Taille des mailles (dx projeté sur les axes)
2
Voisins des mailles
· Nombre d'éléments voisins des mailles
· Indices des mailles voisines pour chaque Maille
3
Arêtes
· Nombre d'arêtes
· Nombre d'arêtes par maille
· Indices des Arêtes pour chaque Maille
· Type de CL d'une arête (valeurs dépendant du solveur)
· Normale à l'arête
· Nombre de mailles voisines de l'arête et leurs indices. En MODULEF, on a toujours le même nombre de voisins que d'arêtes dans les mailles, mais on a des éléments voisins nuls, qui donnent les mailles de bord.
· Nombre de nœuds par arêtes et leurs indices
· Longueur (surface en 3D) de l'arête
· Coordonnées des centres des arêtes
Variables privées:
- éléments de base des arêtes (ces éléments sont supprimés après le calcul complémentaire des arêtes car on ne les réutilise pas après)
- éléments de base des mailles : coordonnées barycentriques, déterminant du triangle ou tétraèdre
Fonctions publiques :
- Constructeurs
- Constructeur Boite : avec la gestion, un nom de maillage, avec la dimension, le nombre de maille et le nombre de nœuds : alloue les éléments de maillage (publiques et privés).
- Constructeur Maître : avec la gestion, un nom de maillage, un fichier de maillage ouvert et la dimension pour créer les maillages avant lecture. Puis on lit le fichier de maillage, on calcul les données complémentaires arêtes et mailles. On ne se sert plus des données complémentaires arêtes ?
- Méthodes :
- Récupération des données (pour connexion avec Parallele).
- Fonction booléenne d'appartenance d'un point à une maille
- Ecriture d'un maillage volumes finis de type MODULEF
- Affichage du nom du maillage
- Accès à la dimension, au nombre de mailles, au nombre de nœuds, au nombre de Nœuds pour chaque Maille, aux indices des Nœuds pour chaque Maille, aux coordonnées des Centres des Mailles, aux Coordonnées des Nœuds, à la surface des mailles, à la taille des Mailles, au nombre et indices des éléments voisins des mailles, aux nombre d'arêtes par maille, au Type de CL d'une arête , au vecteur normal à l'arête au nombre et indices des mailles voisines de l'arête, au nombre et indices des nœuds par Arête, à la longueur (surface en 3D) de l'arête, aux coordonnées des Centres des Arêtes.
Fonctions protégées
- Calculs complémentaires des Arêtes barycentriques :
- appel du calcul des centres
- Calcul des sous-éléments des arêtes (découpées à partir de leur barycentre)
- Calcul des normales aux arêtes
- Calcul des surfaces/longueurs des arêtes
- Calculs complémentaires des Mailles (surcharge de la fonction de Maillage) :
- appel du calcul des centres,
- Calcul des sous-éléments des mailles (découpées à partir de leur barycentre),
- calcul des surfaces et des DX des mailles,
- destruction des éléments de base des arêtes.
- Calcul des centres des arêtes,
- Calcul des centres des mailles.
- lecture d'un maillage type MODULEF
Fonctions privées
- Calcul des éléments de base : coordonnées barycentriques, équation cartésienne, surface de l'élément
- Calcul des sous-déterminants d'une matrice de point d'un sous-élément (procédure récursive). Ne fonctionne pas si la matrice est de dimension 1.
- Nom du maillage
- affichage du nom
- Mettre à zéro le maillage
3.5.2.0.2 Classe MaillageVF
hérite de Maillage
Description des maillages
Variables protégées:
- Nombre d'Arêtes possèdant un voisin à Gauche et à Droite, et leurs indices
- Nombre d'Arêtes ne possédant pas de voisin à Droite, et leurs indices
- Nombre d'Arêtes ne possédant pas de voisin à Gauche, et leurs indices
Fonctions publiques
- Constructeurs
- Constructeur Boite. avec la gestion, un nom de maillage, avec la dimension, le nombre de maille, le nombre de nœuds et le nombre d'arêtes : alloue les éléments de maillage (publiques et privés).
- Constructeur Maître. avec la gestion, un nom de maillage et la dimension pour créer les maillages avant lecture.
- Méthodes
- Affiche le nom du maillage
- Accès au nombre et indices des Arêtes possédant un voisin à Gauche et à Droite,
- Accès au nombre et indices des Arêtes ne possédant pas de voisin à Gauche,
- Accès au nombre et indices des Arêtes ne possédant pas de voisin à Droite.
Fonction protégées :
- Création des tableaux de voisins
- Destruction de ces tableaux avant nouveau calcul.
Fonctions privées :
- Nom du maillage
- affichage du nom
- Mettre à zéro le maillage
3.5.2.0.3 Classe Boite
objet des éléments par zones réparties et superposables
Variables protégées:
- numéro identifiant,
- dimension de la boite
- coordonnées dans le domaine,
- éléments contenus :
- nombre d'éléments,
- nombre de champs ( indices régis par le Modele )
- Nombre de pas sauvés (passées, présentes et futures - indices régis par le Solveur),
- valeurs physiques
- sous-boites de bord lui appartenant,
- coordonnées de l'intérieur (le complémentaire des sous-boites),
- nombre et liste des éléments intérieurs (non contenus dans une sous-boite),
- nombre et liste des id zones de couplage attachées,
Variables privées:
- objet maillage attaché,
- objet parallele attaché,
- objet modèle attaché,
- objet solveur attaché.
Fonctions publiques :
- deux types de constructeurs :
- soit avec lecture d'un fichier de données,
- soit avec attente des données par communication.
Fonctions protégées :
- appel parallele pour info Boite
- classement des sous-boites (du plus petit = plus grand nombre d'identifiants, au plus grand = l'intérieur de la boite)
- Calcul des sous-ensembles de l'intérieur et de leurs sous-ensembles voisins
- calcul des indices de champ dans les sous-boites, et dans l'intérieur
Fonctions privées
- définition des sous-boites
- relation avec les objets de modèles (nom des champs, loi) et solveur (flux, calculs)
- aire de la boite
- éléments intérieurs et sous-boites (construction en fonction des boites voisines),
- trouver les voisins (1x pour les VF après (re)maillage) des éléments,
- calculer les flux des éléments internes -> appel schéma,
- intégrer ces flux -> appel schéma,
- modification des grandeurs physiques,
-
itération en temps
 appel schéma solveur sur les données.
appel schéma solveur sur les données.
3.5.2.0.4 Classe Modele
Décrit un modèle type
- Nom du modele
- nombre de grandeurs physiques
- liste des grandeurs : noms
- indice des grandeurs liées : fermeture du système (loi d'état)
- indice de(s?) la valeur(s?) modifiée(s?) par la loi d'état
- énumération des modèles stationnaire ou instationnaire
Méthodes :
- loi d'état nulle
3.5.2.0.5 Classe ModeleEuler
Modèle d'Euler : hérite de la classe Modele
Parmètres Euler :
!c Rapport de chaleurs spécifique (pour l'air = 1,4)
F REAL(DD), PARAMETER :: GAMA = 1.4_DD
!c Vaut simplement GAMA-1
R(KHI) REAL(DD), PARAMETER :: GAMA_1 = 0.4_DD
!c Pression de sortie constante égale à 1 bar
F REAL(DD), PARAMETER :: PA = 105000._DD
- Nom du modele constant : Euler
- liste des grandeurs : noms
- constantes physiques
Méthodes :
- loi d'état d'Euler.
3.5.2.0.6 Classe Solveur
solveur type
Variables protégées :
- Pointeurs sur la Boite, le Maillage et le Modele
- Pas de temps de la prochaine itération
- Nombre de pas de temps à sauver
- indice du temps précédent
- indice du temps présent
- Nombre total de pas de temps
- Temps de départ du calcul
- Temps actuel
- Temps final
- intervalle de temps entre deux sauvegardes/affichages
- dernier temps de sauvegarde
- booléen indiquant si les valeurs des champs sont prises aux nœuds (true) ou au centre des mailles (false).
Variable privée :
- Indicateur de boite attachée
Méthodes :
- Procédure d'attachement sa boite au solveur après sa création
On doit tout d'abord créer le maillage, le modèle, le solveur, avant de créer la boite. On doit ensuite appeler cette fonction pour attacher la boite au solveur.
On ne peut pas exécuter la procédure Calcul_Un_Pas sans avoir exécuter la méthode Attache_Boite qui modifie cet indicateur
· Calcul de schéma numérique type :
o Calcul du pas de temps
o
appel
de la fonction de calcul du schéma Solveur, sans paramètre ![]() la dernière fonction (de l'arbre « SolveurQqChose »)
de calcul, sans paramètre.
la dernière fonction (de l'arbre « SolveurQqChose »)
de calcul, sans paramètre.
o mise à jour des variables : on écrit le temps présent dans le temps passé et le temps futur dans le temps présent
o test des valeurs : grandeurs positives, intervalles de vraissemblance ... (suivant Modele)
o appel sauvegarde/affichage
Fonctions privées :
3.5.2.0.7 Classe SolveurVF
- hérite de la classe Solveur.
- description du solveur (calcul des flux, intégration)
Variables protégées
- indices des variables calculables par le schéma.
Variable privée
- Vecteur de flux temporaire, de taille NbChamps (dépend du Modele)
Méthodes :
- Récupération et écriture des flux
- Mise à zéro du vecteur de flux
Fonctions protégées :
- CalculVF; paramètres
- Fonction de calculs préliminaire : calcul des gradients pour Van Leer, par exemple.
- Fonction de flux 'type' (cf FluxGod ou FluxVL)
Fonctions privées :
3.5.2.0.8 Classe SolveurVFEuler
Solveur VF spécifique au modèle d'Euler
- hérite de la classe SolveurVF,
- attache le modèle d'Euler au solveur,
- Gère les flux.
Paramètres CL Euler :
!c Débit imposé en entrée
REAL(DD), PARAMETER :: Q0 = 450._DD
!c Enthalpie imposé en entrée
REAL(DD), PARAMETER :: H0 = 450000._DD
! Valeur de la normalisation de la pression dans cherche_pm
REAL(DD), PARAMETER :: VALP = 128.5714285714286_DD
Variables protégées
- pointeur modèle d'Euler
- Variables auxiliaires -> on les place dans les champs => futur = now+1 ? (cf besoin d'échange pour parallele ou échange des flux simplement)
- CL Possibles + descriptions
Méthodes :
Fonctions protégées :
- Fonction de Mise à jour de U global
- Fonction de Mise à jour de U incrément - cf ROAUX et EAUX (FLUX_AUX)
- coordonnées (inline) INIT_COORD
- Solveur de Roe (suppression de l'objet spécifique)
- CL ( réfléxion)
- Fonctions de conditions aux limites admissibles
- Mises à jour du vecteur flux correspondants
Fonctions privées :
3.5.2.0.9 Classe SolveurVFEulerGodunov
hérite de la classe SolveurVFEuler.
Utilise un solveur de type Godunov
Solveur VF spécifique au modèle d'Euler
Variables protégées
- rien.
Méthodes :
- CalculVFEulerGodunov : appel de calculVF (de SolveurVF) avec fonctions en paramètre. C'est cette fonction
Fonctions privées :
- Fonction de préliminaires vide
- Fonction de flux
- INIT_UGOD
3.5.2.0.10 Classe Zone
Classe de la zone de calcul (distribuée sur une grappe de PC) Elle encapsule le programme Boite et est CORBAtisée. Elle permet l'échange des données avec le couplage (méthode données - couplage avec structure de zone de couplage). Elle sauvegarde ses données.
Variables protégées :
- nombre de zones de couplage recouvrant la boite int NbZonesCpl;
· identificateurs des zones de couplage recouvrant la boite int* idZonesCpl;
Méthodes
- paramètres du code (Modele et Solveur), lecture
- CI, lecture
- Découpage des boites (pour l'instant régulier)
- Calcule les maillages de chaque boite,
- créé le Modele et le Solveur (suivant chaîne de caractères: switch sur les objets valides - feuilles des arbres de classe Modele et Solveur)
- calcul si la boite est dans une (ou plusieurs) zone de couplage
- lancement du calcul
- Calcul d'une itération
- Envoie les données couplage
- Récupère les données couplage et le pas de temps
- itère
Fonctions privées :
- coordonnées des zones de couplage
3.5.2.0.11 Classe Couplage
Plusieurs zones de couplage.
- On récupère les données de deux zones de calcul :
- boites,
- ss-boites,
- maillages.
- On reconstruit ces objets à partir des données.
- on fait le couplage (dépend du type de maillage : déplacement ou non des mailles => modification des fonctions de couplage) et
- on renvoie les données modifiées aux zones.
Principe du couplage :
! base : couplage
! COUPLAGE : fonction alpha sur la zone de couplage (qui va du
! maillage 1 au maillage 2). Cette fonction passe de 1 à 0, de
! Th1 à Th2.
! ~u1(i,n+1) = alpha1(i) *u1(i,n+1) + (1-alpha1)(i)*Proj21(u2)(i,n+1)
! ~u2(i,n+1) = (1-alpha2)(i)*u2(i,n+1) + alpha2(i) *Proj12(u1)(i,n+1)
! SOLUTION APPROCHEE :
! u( C , n+1) = alpha(i) ~u(C , n) + (1-alpha(j))) ~u(C , n)
! ij 1i 2j
! Projection L1 de la solution calculee 1 sur le maillage 2 (par exemple)
! PI12 (u1) (j.h2) = SOMME(i) MU12(i,j)*u1(i)
! ou :
! MU12(i,j) = M(i,j)/h2
Ces objets contiennent :
Variables protégées :
- coordonnées de la zone de couplage (polygone, autres éléments géométriques ),
- spécification des bords aux limites alpha=0 ou 1,
- boites contenues,
- type de fonction de couplage,
- taille de la bande constante sur les limites,
- 2 maillages (0 et 1) contenus
- fonctions de couplage sur les 2 maillages
Fonctions :
- Calcul fonction de couplage type
- Calcul zone de couplage (produit matrice vecteur)
- Calcul intersections zone de couplage type
On prend le max de la fonction de couplage, pour les intersections entre les zones de couplage.
3.5.2.0.12 Classe CouplageVFVF
hérite de la classe Couplage.
Cette classe sert à calculer la fonction de couplage pour des VF, les intersections entre deux maillages VF et la modification des valeurs.
Fonctions :
- Calcul fonction de couplage type
- Calcul intersections zone de couplage VF-VF
3.5.2.0.13 Classe Gestion
Cet objet est utilisé pour le deboggage et l'application à de gros calculs. Ils gèrent la mémoire et les exceptions utilisées par les processus. A chaque allocation de tableau important, on ajoute le pointeur sur ce tableau, ainsi que la mémoire qu'il utilise. Lorsque l'on désalloue ce tableau, l'objet vérifie qu'il a bien été répertorié dans le tableau de pointeurs mémoire.
De même, à chaque construction d'un nouvel objet quelconque, on déclare la liste de ses exceptions à l'objet de gestion associé au processus. Cela permet en cas d'erreur de renvoyer une exception dans la variable publique Exception et d'afficher l'erreur ainsi déclarée à l'aide de la fonction d'affichage. Surtout, cette erreur est spécifique à l'objet qui la déclenche. Le nom de cet objet est déclaré lui aussi et affiché en cas d'erreur.
Dans chaque classe, on place :
- en privé un pointeur vers la classe de Gestion du processus,
- (construit, à remplir) en privé des exceptions renvoyées par chaque méthode de la classe.
- initialisation de Gestion dans les constructeurs.
- la liaison du pointeur de Gestion, avec l'objet de Gestion du processus
- la déclaration des exceptions
- la déclaration du nom de l'objet.
- des réels : définition du type MonReel (simple ou double) pour les calculs
- de la mémoire d'un code : tableau de pointeurs (convertis en entiers) vers les variables allouées et compteur de taille de la mémoire utilisée.
- des exceptions : Pour chaque objet du process, on déclare des valeurs d'exceptions, leur nom et la chaine d'erreur correspondante. La fonction renvoie un numéro de décalage spécifique à l'objet. On pourra ainsi traiter les exceptions renvoyées par tout objet et retrouver celui-ci.
L'objet de Gestion gère lui-même ses propres exceptions.
On pourra rajouter :
- la définition d'un ErrHandler, -> oui car il affichera la pile d'exceptions lancée, fermera proprement MPI (et CAST?) et quittera.
- le niveau de danger d'une fonction et des exceptions définies.
Fonctions :
- Lancement d'une exception
- Affichage de la pile d'exceptions lancées
- réaction du code : ErrHandler (gestion arrêt brutal) =>
- appels aux communicateurs,
- correction possible,
- réaction utilisateur
En-tête spécifique à cette classe et valable pour toutes les autres : voir EGlobal.hh
3.5.2.0.14 Classe SSBoite
Classe des sous-boites des intersections des boites,
Règle les problèmes d'intersections entre les boites. Pour tenir compte des recouvrements, on ne calcule que les flux rentrant dans la sous-boites, par rapport à la boite. La sous-boite est dupliquée pour chacune des boites qui la définie.
Variables protégées:
- pointeur sur le tableau des éléments de la boite
- identifiant boite concernée (= num du proc),
- identifiant des n boites voisines,
- identifiant global de sous-boite (du type [n,boite1,boite2,..,boiten], avec boite1 < boite2 < ... < boiten, pour l'unicité),
- type de sous-boite (angle ou bord),
- éléments-maillages inclus
- pointeur sur la sous-boite mère (NULL si sous-boite mère = boite)
-
liste des sous-boites contenues (si NULL
 feuille),
feuille), - liste des éléments intérieurs (non contenus dans une sous-boite),
- indices des arêtes à traiter par cette sous-boite (arêtes orientées intérieures ).
Variables privées:
Fonctions publiques :
- récupération ou calcul des indices des arêtes à calculer par cette sous-boite (orientées rentrant et sortant de la boite - voir la normale au bord ou au coin de la boite),
- calculer les flux orientés d'un élément,
- intégrer ces flux (après communications - test)
Fonctions protégées Fonctions privées
3.5.2.0.15 Classe Parallele
Communications entre les boites et entre les zones de couplage :
Un objet parallèle pour chaque boite. Gère toutes les communications MPI entre les sous-boites
Dans parallèle, on construit
- des tableaux de renumérotation des arêtes à Gauche et à Droite - seulement : c'est le plus gros calcul. Cela implique que l'on fait les calculs des conditions aux limites en premier dans le calcul des flux, puis que l'on calcul les arêtes qui ne sont pas au bord, dans les procédures de calcul des flux (fait pour Godunov).
- On se fixe la règle : une arête est dans une sous-boite, si ses deux éléments voisins sont dans la sous-boite.
- On place d'abord les arêtes des SSSboites (intersection de deux sous-boites de coin).
- Ensuite, on met celles des SSBoites.
- Enfin les arêtes intérieures.
- Une classification des SSSBoites et des SSBoites : Pour chaque SSSBoite et SSBoite (et l'intérieur de la Boite), on indique l'indice de la première arête dans un tableau (parallèlisation du calcul des flux aux travers des arêtes).
- 1 méthode d'appel de ces indices get_TABGD. On teste :
- si l'arête demandée est la première de l'une des SSSBoites. Si oui, on communique la SSSBoite précédente (si elle existe).
- idem on teste si l'arête est la première de l'une des SSBoites. Si oui, on communique la SSBoite précédente (ou la SSSBoite si le SSBoite est la première de la liste.
- enfin, si l'arête est la première de l'intérieur de la boite, on envoie la dernière sous-boite.
- Comme cela, on calcule les intérieurs des boites en dernier et on est sûr que les communications MPI sont terminées lorsque l'on met à jour globalement les champs sur toute la boite.
Variables protégées :
- tableau des ssboites et des proc associés
- communicateurs ssboites-ssboites
- indices locaux <-> indices globaux
- indices des premières arêtes des sssboites, ssboites et boites
- tableau des arêtes à gauche et à droites (sans CL)
Constructeurs
- Constructeurs possibles :
- avec passage des arguments du Maître : construction avec lancement de MPI, numéro du proc.
- avec liste de processus : construction d'un groupe de communication pour la parallélisation.
Méthodes
- récupérations :
- envoie global des paramètres (Modele et Solveur) de Zone
- récupère Modele et Solveur
- envoie les maillages de chaque boite
- récupère le maillage local et calcul les indices locaux
- envoie des boites et ss-boites
- reçoit boite : attendre le calcul des boites et recouvrements du master, reçois les coordonnées d'une boite (id, CoordBoite, nbelts, ssboites, nbeltsinter, ), données ``Boite'' et ``SSBoite'', Pa->Recoit_Boite(Info_Boite);
- envoie des données globales (éléments) pour chaque boite
- recoit éléments : recevoir les éléments de la boite ou de la sous-boite (elts total, indices, indices elts interieurs)
- reçoit couplage : données ``Couplage'' (ma boite est-elle dans une ou plusieurs zones de couplage ?
Fonctions privées :
- modification des boites : envoie des éléments en fonction des nouvelles coordonnées.
- Calcul des indices des arêtes modifiés et modification des indices global->local de maillage, -> dépend des solveurs (eulériens, lagrangiens),
4. Conclusion
L'utilisation de la programmation objet (c++), qui a entraîné une transformation complète de mon code de couplage FORTRAN 90, ainsi que la construction d'un code fluide en 3 dimensions (et non pas en 2D) ont été des freins sévères pour la réalisation de cas test sur la grille de grappe pendant la durée du stage post-doctoral (dont la durée n'était que de six mois). Je continue néanmoins à implémenter le code et espère lancer ces calculs avec l'aide de Toan Nguyen prochainement.
Nous avons beaucoup insisté, dans ce travail, sur la nécessité, pour un code de calcul parallélisé généraliste optimum, de contrôler le recouvrement des phases de communication par celles de calcul. Cette optimisation n'est pas anodine : un code permettant d'effectuer des calculs de couplage doit non seulement être réfléchi en terme d'analyse numérique, mais aussi d'informatique, à cause de la taille toujours croissante des modélisations auxquelles on le destine.
Enfin, nous avons construit un mécanisme de contrôle dynamique à l'exécution par l'intermédiaire de l'objet de Gestion. Il reste cependant à implémenter la visualisation du calcul en temps réel (avec le logiciel AVS utilisé dans d'autres projets INRIA). La réalisation ces fonctionnalités est impérative pour le numéricien qui teste le code, ou le scientifique qui l'utilise. Il semble important de réfléchir - dans ces deux domaines - sur une hiérarchisation respectivement des paramètres à modifier ou des grandeurs à afficher, en fonction de leurs impacts en espace (très locaux, locaux ou globaux).
Bibliographie
Steger J.L. Bernek J.A. and Dougherty F.C.
``A flexible grid embedding technique with application to the Euler equations''.
AIAA
, (831944), 1983.
Bernard Pierre-Eric.
``Parallélisation et multiprogrammation pour une application
irrégulière de dynamique moléculaire opérationnelle''
.
PhD thesis, Lab.
Modélisation et Calcul de l'Institut d'Informatique et de Mathématique
Appliquées, 1997.
Kreiss H.-O.
``Construction
of a curvilinear grid''.
SIAM J. Sci.
Stat. Comput., 4(2):270-279, 1983.
Lacôme J.L.
``Analyse de la méthode Particulaire; Application à la
détonique''.
PhD thesis, INSA Toulouse, Nov. 1997.
Lanson N.
``Etude des Méthodes Particulaires Renormalisées. Application
aux problèmes de dynamique rapide''.
PhD thesis, INSA Toulouse, Dec. 2000.
Mancip M.
Couplage de méthodes numériques pour les lois de conservation.
Application au calcul de l'injection.
PhD thesis, INSA - Lab.
MIP, 2001.
Pärt-Enander E.
``Overlapping
Grids and Applications in Gaz Dynamics''
.
PhD thesis, Dep. of Scientific Computing, Uppsala Univ., 1995.
Pärt-Enander E. and Sjögreen B.
``Conservative and non-conservative interpollation between overlapping
grids for finite volume solutions of hyperbolic problems''.
Comp. Fluid, 23(3):551-574, 1994.
Starius G.
``Composite mesh difference methods for elliptic boundary value problems''.
Numerical Mathematics, 28:243-258, 1977.
2002-06-27
![\includegraphics[width=14cm,height=8.5cm]{/home/mancip/XFIG/POST-DOC/FluideGlobale2.eps}](img1b.gif)
![\includegraphics[width=14cm,height=8.5cm]{/home/mancip/TEX/post-doc/images/echange_donnees.eps}](img3.gif)
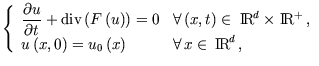
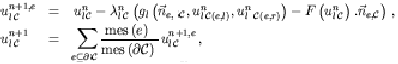

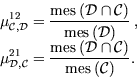
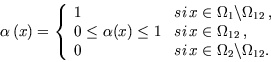
![\includegraphics[width=8cm,height=8cm]{/home/mancip/TEX/THESE/REDAC/IMAGES/alpha.eps}](img27.gif)
![\includegraphics[width=8.2cm,height=8.5cm]{/home/mancip/TEX/THESE/REDAC/IMAGES/schmproj5.eps}](img37.gif)
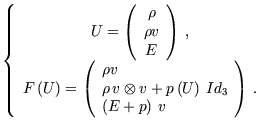
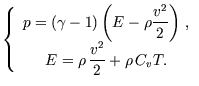
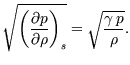
![\includegraphics[width=12cm,height=10cm]{/home/mancip/TEX/post-doc/images/figure1_0.eps}](img58.gif)
![\includegraphics[width=12cm,height=10cm]{/home/mancip/TEX/post-doc/images/figure1_1.eps}](img59.gif)
![\includegraphics[width=15cm,height=7cm]{/home/mancip/TEX/THESE/REDAC/IMAGES/dispositif.eps}](img60.gif)
![\includegraphics[width=15cm,height=13cm]{/home/mancip/TEX/THESE/REDAC/IMAGES/COUPLAGE/DFG/images003.ps}](img61.gif)
![\includegraphics[width=15cm,height=13cm]{/home/mancip/TEX/THESE/REDAC/IMAGES/COUPLAGE/DFG/images013.ps}](img62.gif)
![\includegraphics[width=15cm,height=13cm]{/home/mancip/SOUTENANCE/ANIM/anim_zone_cpl14.ps}](img63.gif)
![\includegraphics[width=15cm,height=9.5cm]{/home/mancip/TEX/post-doc/IMAGES/chocCoin.eps}](img66.gif)
![\includegraphics[width=15cm,height=10.5cm]{/home/mancip/TEX/post-doc/IMAGES/chocCoin1.eps}](img68.gif)
![\includegraphics[width=17cm,height=9.5cm]{/home/mancip/TEX/post-doc/IMAGES/organisationBoites.eps}](img69.gif)
![\includegraphics[width=12cm,height=10cm]{/home/mancip/TEX/post-doc/IMAGES/organisationBoites1.eps}](img70.gif)
![\includegraphics[width=15cm,height=10.5cm]{/home/mancip/TEX/post-doc/IMAGES/organisationBoitesDeform.eps}](img73.gif)
![\includegraphics[width=15cm,height=10.5cm]{/home/mancip/TEX/post-doc/IMAGES/organisationBoites1Deform.eps}](img74.gif)
![\includegraphics[width=13cm,height=9cm]{/home/mancip/TEX/post-doc/images/construct_sous-boites.eps}](img75.gif)
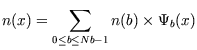
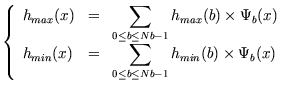
![\includegraphics[width=14.142cm,height=9cm]{/home/mancip/TEX/post-doc/Classes.eps}](img81.gif)